6.3 선형/이진 탐색(Linear/Binary search)
6.3.1 선형 탐색(Linear Search)
- 특정 값을 주어진 벡터 공간에서 찾기 위해 저장 공간을 순차적으로 비교하면서 찾는 방식
- 가장 단순하고 직관적인 검색 방법
- Sequential search
Pseudocode
- 찾고자 하는 값을
k라고 할 때,for i 1 to nif x[i] == k then return i
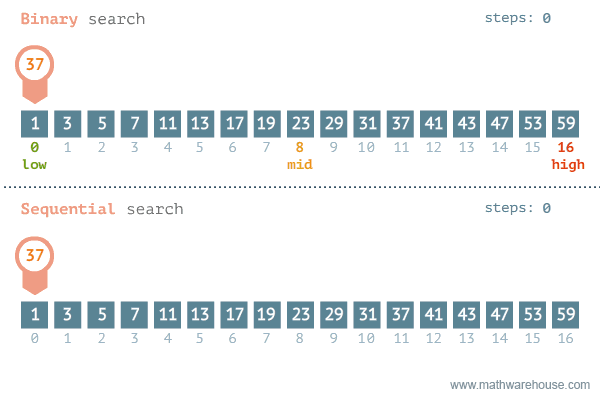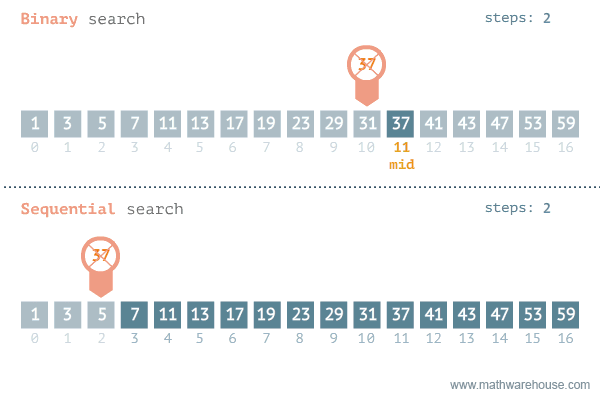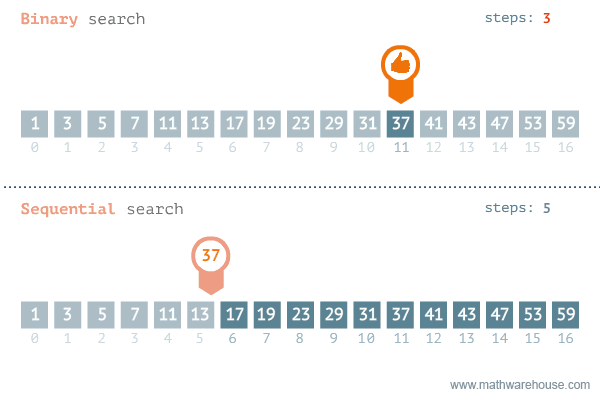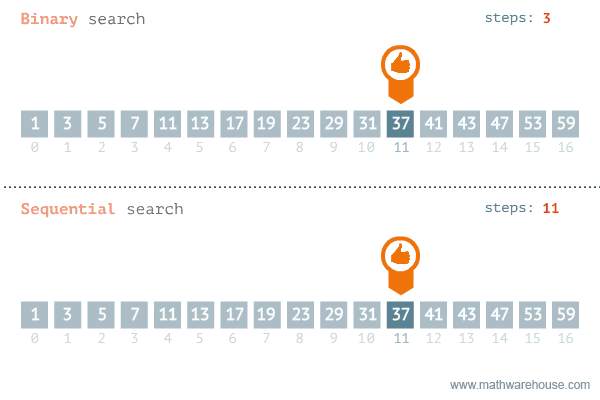
6.3.2 이진 탐색(Binary Search)
- 정렬된 벡터에서 특정 값을 탐색하기 위한 알고리즘
- 전체 탐색범위를 반으로 나눈 후 찾고자 하는 값이 없는 쪽을 버린 후 나머지 부분에서 값을 검색하는 과정을 반복
- 선형 탐색보다 대부분의 경우에서 효율적임(빠름).
Pseudocode: 자연어
- 주어진 배열의 가운데(중앙)에서 시작
- 찾고자 하는 목표값과 배열의 중앙 위치 값과 비교
- 만약 목표값과 중앙 위치값이 같다면 반복을 멈춤
- 목표값이 배열의 중앙 위치값 보다 작다면 가장 작은 인덱스에서 중앙 인덱스 보다 하나 작은 인덱스 까지 값(새로운 최대 인덱스)으로 범위를 측소 후 비교
- 목표값이 배열의 중앙 위치값 보다 크다면 중앙 인덱스에 1을 더한 인덱스 (새로운 최소 인덱스)부터 최대 인덱스 범위로 축소 후 비교
Pseudocode
- 배열 인덱스에 대한 중앙 인덱스(mid = (min + max)/2) 계산
- while min <= max
- mid = floor((min + max)/2)
- if vec[mid] == target then return(mid)
- else if vec[mid] > target
- then update max <- mid - 1
- else update min <- mid + 1
구현
# Binary search
binary_search <- function(target, ovec) {
maxL <- length(ovec) # 벡터의 길이
minL <- 1L # 시작
while (minL <= maxL) {
midL <- floor((minL + maxL)/2)
if (ovec[midL] == target) {
return(midL)
} else if (ovec[midL] > target) {
maxL <- midL - 1
} else {
minL <- midL + 1
}
}
return(NULL)
}
x <- seq(1, 40000000, by = 3)
set.seed(2)
k <- sample(x, 1)
binary_search(target = k, ovec = x)[1] 5551055재귀함수를 이용한 구현
# 재귀함수를 활용한 binary search
rbinary_search <- function(target, ovec, minL, maxL) {
if (maxL <= minL) return(NULL)
midL <- floor((minL + maxL)/2)
if (ovec[midL] > target) {
rbinary_search(target, ovec, minL = minL, maxL = midL - 1)
} else if (ovec[midL] < target) {
rbinary_search(target, ovec, minL = midL + 1, maxL = maxL)
} else return(midL)
}
x <- seq(1, 40, by = 3)
set.seed(2)
k <- sample(x, 1)
rbinary_search(target = k, ovec = x, minL = 1, maxL = length(x))[1] 56.3.3 선형탐색과 이진탐색 비교
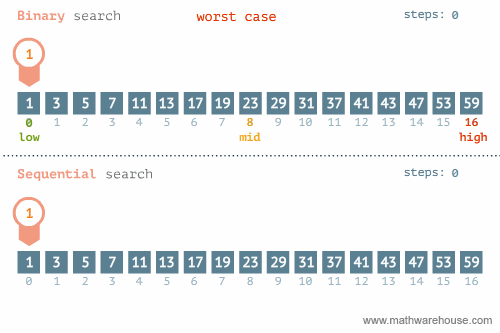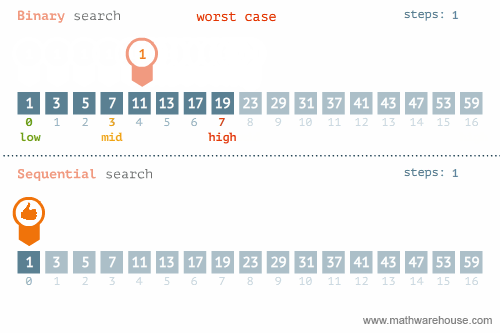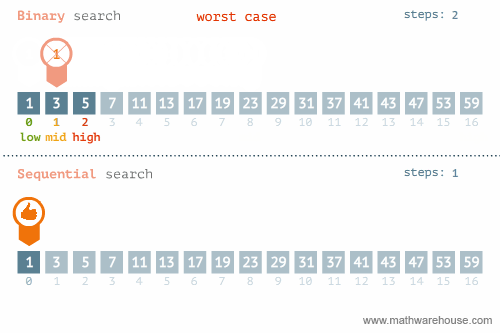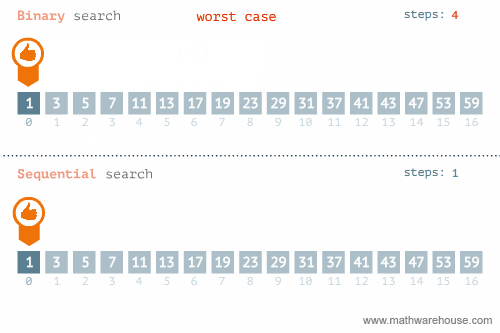
이진탐색이 안좋은 경우: https://blog.penjee.com/binary-vs-linear-search-animated-gifs/ 에서 발췌

이진탐색 성능이 가장 좋은 경우: https://blog.penjee.com/binary-vs-linear-search-animated-gifs/ 에서 발췌