6.2 재귀함수(Recursive function)

함수 자신을 다시 호출하는 함수로 직관적으로 이해하기 쉽고 간결함

  • 재귀함수 작성 시 재귀호출을 탈출하는 조건을 명확히 하는 것이 관건

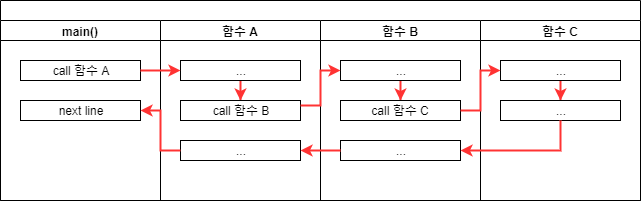
일반적 함수의 호출 및 리턴 과정

http://10bun.tv/beginner/episode-4/ 에서 발췌

  • main() 함수 안에서 함수 A가 호출되면, 코드 진행은 함수 A의 처음으로 옮겨짐.
  • 마찬가지로 함수 A 내부에서 함수 B가 호출되면서 코드 진행은 함수 B의 처음으로 옮겨짐.
  • 함수 B가 진행되면 중간에 함수 C가 호출되면서 함수 C의 처음으로 진행이 옮겨짐
  • 함수 C가 모든 실행을 마치면 함수 B에서 C를 호출했던 다음 줄로 돌아감(return)
  • 함수 B의 모든 실행을 마치면 함수 A에서 B를 호출했던 다음 줄로 돌아감(return)
  • 함수 A의 모든 실행을 마치면 main() 함수에서 A를 호출했던 다음 줄로 돌아감(return)

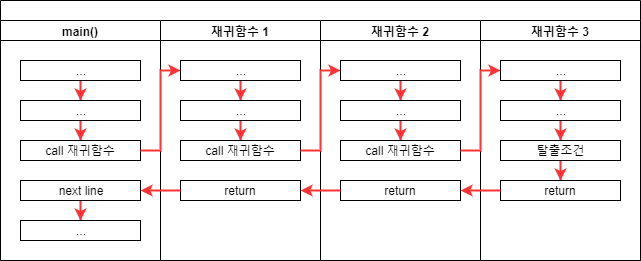
재귀 함수의 호출 및 리턴 과정

http://10bun.tv/beginner/episode-4/ 에서 발췌

  • 모든 재귀함수의 호출 시 새로운 작업공간(메모리)을 확보해 진행
  • 동일한 코드가 작업공간만 옮겨 다니며 무한히 반복되는 구조이기 때문에 탈출조건이 필요

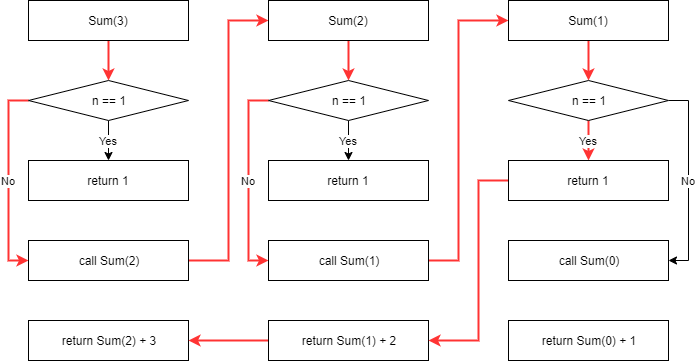
예제1: 재귀함수를 이용한 1부터 n 까지 합을 구하는 함수

recursive_sum <- function(n) {
  if (n == 1)  return(n) # 종료 조건 
  return(n + recursive_sum(n-1))
}

recursive_sum(3)
[1] 6

http://10bun.tv/beginner/episode-4/ 에서 발췌

  • recursive_sum(3) 실행 시 n이 1이 아니기 때문에 recursive_sum(2) 호출
  • recursive_sum(2) 실행 시 n이 1이 아니기 때문에 recursive_sum(1) 호출
  • recursive_sum(1) 이면 n == 1 을 만족하기 때문에 1 반환(return)
  • recursive_sum(2)는 recursive_sum(1)에서 반환 받은 1과 n = 2을 더해서 3을 반환(return)
  • recursive_sum(3)은 recursive_sum(2) 에서 반환 받은 3과 n = 3을 더해서 6을 반환 \(\rightarrow\) 종료

예제2: 계승(factorial) 계산하기

\[ n! = \begin{cases} n \times (n - 1)!, & n=1, \cdots \\ 1, & n = 0 \end{cases} \]

\(f(n) = n!\) 이라고 하면 \(f(n)\)은 아래와 같이 나타낼 수 있음.

\[ n! = \begin{cases} n \times f(n-1), & n=1, \cdots \\ 1, & n = 0 \end{cases} \]

위 식을 이용해 \(3!\)을 구하는 과정: - \(f(3) = 3\times f(2) = 3\times 2 \times f(1) = 3 \times 2\times 1\times f(0) = 3\times 2\times 1\times 1 = 6\)

f(3) = 3*f(2)
         f(2) = 2 * f(1)
                    f(1) = 1

위 과정을 함수로 구현

factorial_manual <- function(n) {
  # browser()
  if (n == 0) return(1)
  return(n * factorial_manual(n-1))
}

# test
factorial_manual(3)
[1] 6
factorial_manual(10)
[1] 3628800
# R 내장함수로 검증
factorial(10)
[1] 3628800

확장예제: 하노이 탑(tower of Hanoi)

“인도 바라나시에 있는 한 사원에는 세상의 중심을 나타내는 큰 돔이 있고 그 안에 세 개의 다이아몬드 바늘이 동판 위에 세워져 있습니다. 바늘의 높이는 1 큐빗이고 굵기는 벌의 몸통만 합니다. 바늘 가운데 하나에는 신이 64개의 순금 원판을 끼워 놓았습니다. 가장 큰 원판이 바닥에 놓여 있고, 나머지 원판들이 점점 작아지며 꼭대기까지 쌓아 있습니다. 이것은 신성한 브라흐마의 탑입니다. 브라흐마의 지시에 따라 승려들은 모든 원판을 다른 바늘로 옮기기 위해 밤낮 없이 차례로 제단에 올라 규칙에 따라 원판을 하나씩 옮깁니다. 이 일이 끝날 때, 탑은 무너지고 세상은 종말을 맞이하게 됩니다.”

Wikipedia 발췌

문제: 3개의 기둥 A, B, C가 있고, 기둥 A에 \(N\) 개의 원판이 크기 순서대로 쌓여져 있을 때(제일 밑에 원판이 가장 큼), 모든 원판을 기둥 C로 옮기기

조건

  • 한 번에 하나의 원판만 옮길 수 있음
  • 큰 원판이 작은 원판 위에 있으면 안됨
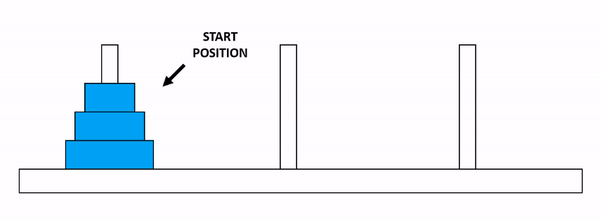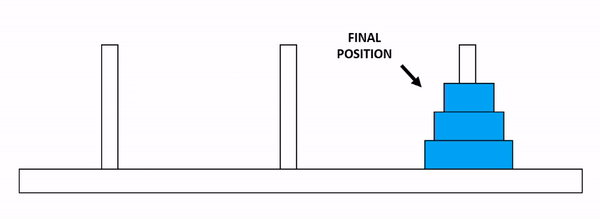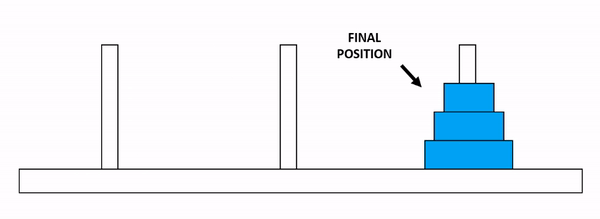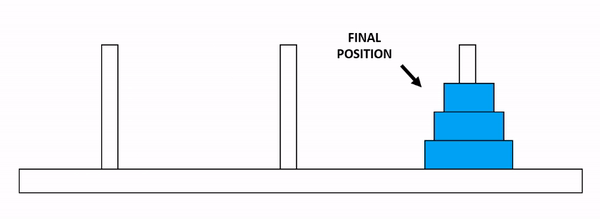
하노이 탑 문제

Figure 6.2: 하노이 탑 문제

Solution

원판의 크기가 제일 작은 것 부터 큰 것 까지 각각 1, 2, 3 번을 부여 했을 때

  • 1 번 원판을 봉 A에서 C로 옮김 (A \(\rightarrow\) C)
  • 2 번 원판을 봉 A에서 B로 옮김 (A \(\rightarrow\) B)
  • 1 번 원판을 봉 C에서 B로 옮김 (C \(\rightarrow\) B)
  • 3 번 원판을 봉 A에서 C로 옮김 (A \(\rightarrow\) C)
  • 1 번 원판을 봉 B에서 A로 옮김 (B \(\rightarrow\) A)
  • 2 번 원판을 봉 B에서 C로 옮김 (B \(\rightarrow\) C)
  • 1 번 원판을 봉 A에서 C로 옮김 (A \(\rightarrow\) C)

원판이 3개인 경우 총 7번의 이동이 필요 \(\rightarrow\) \(n\)개의 원판이 있을 경우 \(2^n - 1\) 번의 이동이 필요

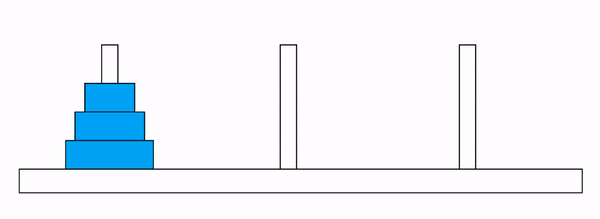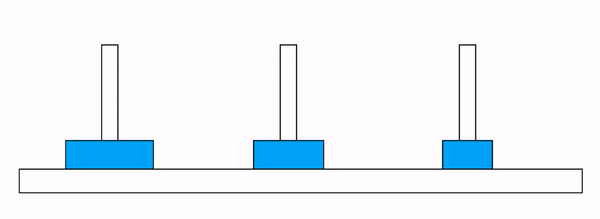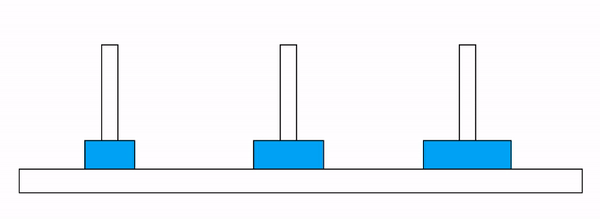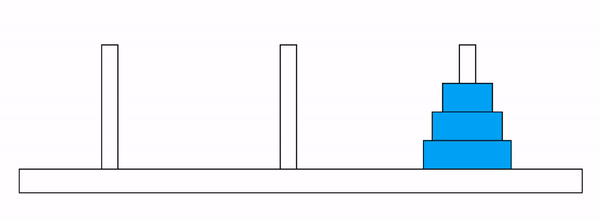
하노이 탑 문제

Figure 6.3: 하노이 탑 문제

알고리즘 구현

move_hanoi <- function(k, from, to, via) {
 # browser()
 if (k == 1) {
   print(sprintf("%d 번 원판을 %s 에서 %s 로 이동", 1, from, to))
 } else {
   move_hanoi(k - 1, from = from, to = via, via = to)
   print(sprintf("%d 번 원판을 %s 에서 %s 로 이동", 
                 from = k, 
                 to = from, 
                 via = to))
   move_hanoi(k - 1, from = via, to = to, via = from)
 }
}


move_hanoi(3, "A", "C", "B")
[1] "1 번 원판을 A 에서 C 로 이동"
[1] "2 번 원판을 A 에서 B 로 이동"
[1] "1 번 원판을 C 에서 B 로 이동"
[1] "3 번 원판을 A 에서 C 로 이동"
[1] "1 번 원판을 B 에서 A 로 이동"
[1] "2 번 원판을 B 에서 C 로 이동"
[1] "1 번 원판을 A 에서 C 로 이동"
move_hanoi(4, "A", "C", "B")
[1] "1 번 원판을 A 에서 B 로 이동"
[1] "2 번 원판을 A 에서 C 로 이동"
[1] "1 번 원판을 B 에서 C 로 이동"
[1] "3 번 원판을 A 에서 B 로 이동"
[1] "1 번 원판을 C 에서 A 로 이동"
[1] "2 번 원판을 C 에서 B 로 이동"
[1] "1 번 원판을 A 에서 B 로 이동"
[1] "4 번 원판을 A 에서 C 로 이동"
[1] "1 번 원판을 B 에서 C 로 이동"
[1] "2 번 원판을 B 에서 A 로 이동"
[1] "1 번 원판을 C 에서 A 로 이동"
[1] "3 번 원판을 B 에서 C 로 이동"
[1] "1 번 원판을 A 에서 B 로 이동"
[1] "2 번 원판을 A 에서 C 로 이동"
[1] "1 번 원판을 B 에서 C 로 이동"