6.4 정렬 알고리즘(Sorting Algorithms)

정렬 알고리즘은 특성에 따라 안정 정렬(stable sort)과 불안정 정렬(unstable sort) 로 구분

정렬의 안정적 특성: 정렬되지 않은 상태에서 중복값이 존재하는 경우 정렬 후에도 그 순서가 그대로 유지

안정 정렬(stable sort): 임의 배열(벡터)에 중복된 값이 존재하는 경우 정렬 후에도 입력 순서와 동일하게 정렬

불안정 정렬(unstable sort): 처음 입력된 중복된 값의 순서가 정렬 후에도 유지된다는 보장이 없음

다음부터 소개할 정렬 알고리즘은 모두 오름차순 정렬을 기준으로 설명

6.4.1 버블 정렬(Bubble Sort)

서로 인접한 두 원소를 비교해 정렬하는 알고리즘

인접한 두 개의 값을 비교해 크기가 순서대로 입력되어 있지 않다면 서로 교환

버블정렬 원리: 위키피디아에서 발췌

첫 번째 자료와 두 번째 자료, 두 번째 자료와 세 번째 자료, … 형태로 마지막 (n-1) 번째 자료와 마지막 자료를 비교해 교환하면서 자료 정렬

첫번 째 순회가 끝난 후 가장 큰 값은 맨 뒤로 이동

순회가 거듭될 때마다 정렬에서 제외되는 원소가 하나씩 증가 \(\rightarrow\) 순회가 거듭될 때 마다 비교 횟수가 줄어듬 \(\rightarrow\) 모든 원소를 방문할 필요가 없음

원소의 이동이 거품이 수면으로 올라오는 듯한 모습을 보이기 때문에 bubble sort라 명칭

버블정렬 애니메이션: 위키피디아 발췌

Pseudocode

데이터(벡터) 입력

주어진 벡터의 인덱스가 i=1부터 i + 1 번째 원소와 비교

i 번째 인덱스의 원소가 i+1 번째 인덱스 원소보다 크다면 서로 교환 (반대의 경우 서로 교환하지 않음)

i를 증가하고 마지막 비교까지 2-3 단계 수행

이미 정렬된 마지막 인덱스는 무시

다시 인덱스 i=1 로 설정 후 2-5 단계 수행

구현

bubble_sort <- function(x) {
  n <- length(x)
  for(i in 1:(n-1)) { 
    for (j in 1:(n - i)) {
      if (x[j] > x[j + 1]) {
        # x[j]가 x[j + 1] 보다 큰 경우 교환
        temp <- x[j]
        x[j] <- x[j + 1]
        x[j + 1] <- temp
      }
    }
  }
  return(x)
}

set.seed(1234)
x <- sample(1:100, 100)
x_sort <- bubble_sort(x)

시간 복잡도

비교 횟수

한 번 순회를 마칠 때 마다 비교 대상이 하나씩 줄어듬. 즉 전체 원소의 개수가 \(n\) 일 때 총 \(n-1\) 번의 순회하면 정렬이 종료됨. 총 원소의 개수가 10개이면, \(9 + 8 + \cdot + 1 = 45\) 번 비교가 수행됨. 즉,

\[ (n - 1) + (n - 2) + \cdots + 1 = \frac{n(n-1)}{2} \]

자리 교환 횟수

최선의 경우: 이미 정렬된 벡터인 경우 자리 교환이 한 번도 이루어지지 않기 때문에 \(\mathcal{O}(n)\) 임.
최악의 경우: 역순으로 정렬된 경우 원소를 비교할 때 마다 자리 교환을 수행해야 하기 때문에 \(\mathcal{O}(n^2)\) 임.

즉 버블 정렬의 시간복잡도는 \(\mathcal{O}(n^2)\)

장점

구현이 쉽고 직관적
정렬하고자 하는 벡터 안에서 교환하는 방식이기 때문에 메모리 공간이 일정함
안정 정렬

단점

시간 복잡도가 비효율적 \(\rightarrow\) 치명적임!!

6.4.2 삽입 정렬(Insertion Sort)

손 안의 카드를 정렬하는 방법과 유사

새로운 카드를 기존의 정렬된 카드 사이에 삽입
새로 삽입될 카드의 수만큼 반복 후 전체 카드가 정렬
자료의 모든 원소를 앞부터 차례대로 이미 정렬된 원소 부분과 비교
매 순서마다 해당 원소를 삽입할 수 있는 위치를 탐색

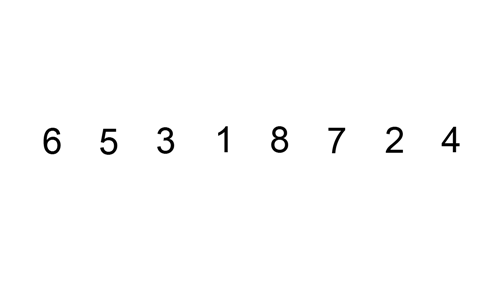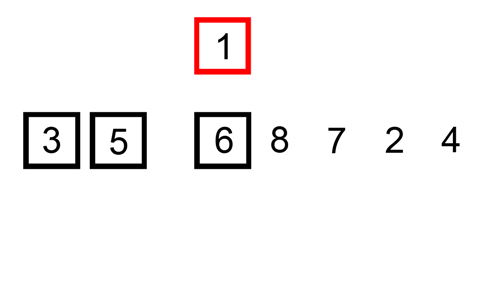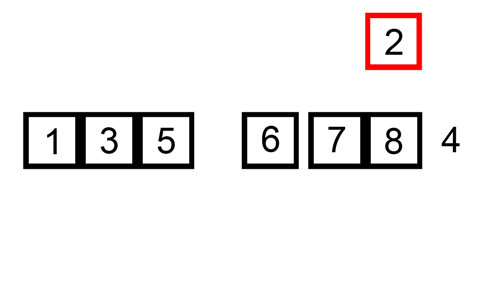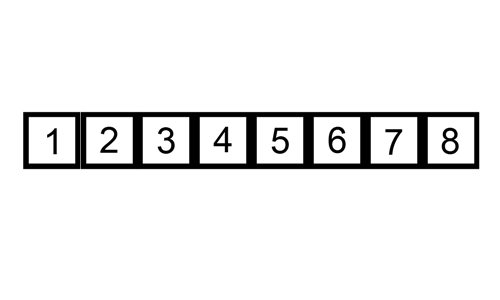
두 번째 원소부터 시작해 앞(왼쪽)의 원소와 비교하면서 삽입 위치 지정 후 자료를 뒤로 옮기고 지정 위치(인덱스)에 원소를 삽입하면서 정렬

두 번째 자료는 첫 번째 자료, 세 번째 자료는 두 번째와 첫 번째 자료, 네 번째 자료는 세 번째, 두 번째, 첫 번째 원소와 비교 후 삽입 위치(인덱스) 탐색

원소가 삽입될 위치를 찾았다면 원소를 한 칸씩 뒤로 이동

삽입정렬 애니메이션: 위키피디아에서 발췌

예시: c(8, 5, 6, 2, 4) 오름차순 정렬

https://gmlwjd9405.github.io/ 에서 발췌

Pseudocode

벡터가 주어졌을 때,

두 번째 인덱스 i=2에 대응하는 원소를 키 값으로 저장

i 바로 앞 인덱스 j = i - 1 지정

j 가 0 보다 크고, j 번째 원소가 키 값보다 크다면

j + 1 번째 원소를 j 번째 원소와 교환

j를 1만큼 감소

4 ~ 6 반복

j + 1 번째 원소를 key 값으로 교환

2 - 8 반복

구현

insertion_sort <- function(x) {
  n <- length(x)
  for (i in 2:n) {
    key <- x[i]
    j <- i - 1
    while(j > 0 && x[j] > key) {
      x[j + 1] <- x[j]
      j <- j - 1
    }
    x[j + 1] <- key
  }
  return(x)
}

set.seed(12345)
x <- sample(1:100, 10)
insertion_sort(x)

 [1] 14 24 51 58 75 80 88 90 92 93

시간복잡도

삽입 정렬을 이해하고 직접 구해보기!!

장점

알고리즘이 단순함
대부분 원소가 이미 정렬되어 있는 경우 매우 효율적임
안정 정렬
버블 정렬에 비해 효율적임

단점

대체로 비효율적(시간 복잡도 확인)

6.4.3 병합 정렬(Merge Sort)

분할 정복(Divide and Conquer)

크고 어려운 문제를 조금씩 쉽게 풀 수 있는 문제 단위로 나눠서 해결 후, 이를 병합해 문제를 해결하는 방식
가장 큰 특징 중 하나는 재귀적으로 호출을 통해 알고리즘 구현

알고리즘 기본설계

Divide (분할): 문제 분할이 가능한 경우 2개 이상의 문제로 나눔
Conquer (정복): 나누어진 문제가 여전히 분할 가능하면 다시 분할 수행. 그렇지 않은 경우 문제를 해결
Combine (결합): 정복한 문제들을 통합해 원래 문제의 답을 도출

분할 정복 알고리즘 구현 시 분할을 어떻게 하는지가 가장 중요함
재귀 호출로 인해 알고리즘의 효율성이 낮아질 수 있음

병합 정렬

주어진 벡터에서 가운데를 나누어 비슷한 크기의 벡터를 두 개로 만든 뒤 이를 재귀 호출을 이용해 각각 정렬 후 정렬된 배열을 하나로 합침.

병합 정렬 과정

벡터(배열)의 길이가 1 또는 2인 경우 이미 정렬이 된 것으로 간주.
그렇지 않은 경우 정렬되지 않은 벡터를 절반으로 나눈 후 비슷한 크기의 부분 벡터 생성
각 부분 벡터를 재귀적으로 병합 정렬 실시
두 개의 부분 벡터를 다시 하나의 벡터로 결합

추가적인 벡터가 필요

각 부분 벡터 정렬 시 합병 정렬을 재귀적으로 호출

합병 정렬 시 정렬이 이루어 지는 시점은 2개 리스트를 합병하는 단계임

구현

분할(`merge_sort()`)

벡터를 2개 부분으로 재귀적으로 나눔 \(\rightarrow\) 벡터의 길이가 1이 될 때 까지

구현을 위해 필요한 요소

주어진 벡터의 첫 번째 인덱스 \(\rightarrow\) 1
주어진 벡터의 마지막 인덱스 \(\rightarrow\) n
주어진 벡터의 가운데 인덱스 \(\rightarrow\) mid = ceiling(n/2)

나누어진 벡터의 왼쪽과 오른쪽 부분을 저장한 객체를 각각left, right로 정의

left: 주어진 벡터의 첫 번째 인덱스에서 mid 번째 인덱스에 해당하는 값을 저장
right: 주어진 벡터의 mid+1 번째 인덱스에서 n 번째 인덱스에 해당하는 값을 저장

이러한 구간을 분할 함수의 인자로 넘겨주는 작업을 재귀적으로 반복

Pseudocode

만약 벡터의 길이가 1보다 크다면,

mid = ceiling(n/2)

left = merge_sort(x[1:mid])

right = merge_sort(x[(mid + 1):n])

병합(`smerge()`)

분할된 벡터를 정렬 후 병합하는 역할 수행

구현을 위해 필요한 요소

정렬한 벡터들을 임시로 저장할 공간(객체): temp
왼쪽과 오른쪽 부분 벡터의 길이 \(\rightarrow\) n1, n2
왼쪽과 오른쪽 부분 벡터의 초기값 저장 \(\rightarrow\) lstart = 1, rstart = 1

Pseudocode (자연어)

왼쪽 부분 벡터와 오른쪽 부분 벡터의 원소를 비교해 더 작은 값이 temp에 저장
만약 left 의 lstart 인덱스에 해당하는 값이 right의 rstart 인덱스에 해당하는 값보다 작다면 temp의 \(i\) 번째 인덱스에 left[lstart] 값 저장 후 lstart 값을 하나씩 증가
반대의 경우 temp의 \(i\) 번째 인덱스에 right[rstart] 값 저장 후 rstart 값을 하나씩 증가

Pseudocode

temp <- numeric(length(left) + length(right))

n1 <- length(left)

n2 <- length(right)

lstart <- 1; rstart <- 1

for (i in 1:length(temp))

   if (left[lstart] <= right[rstart])

     temp[i] <- left[lstart]

     lstart = lstart + 1

   else

     temp[i] <- right[rstart]

     rstart = rstart + 1

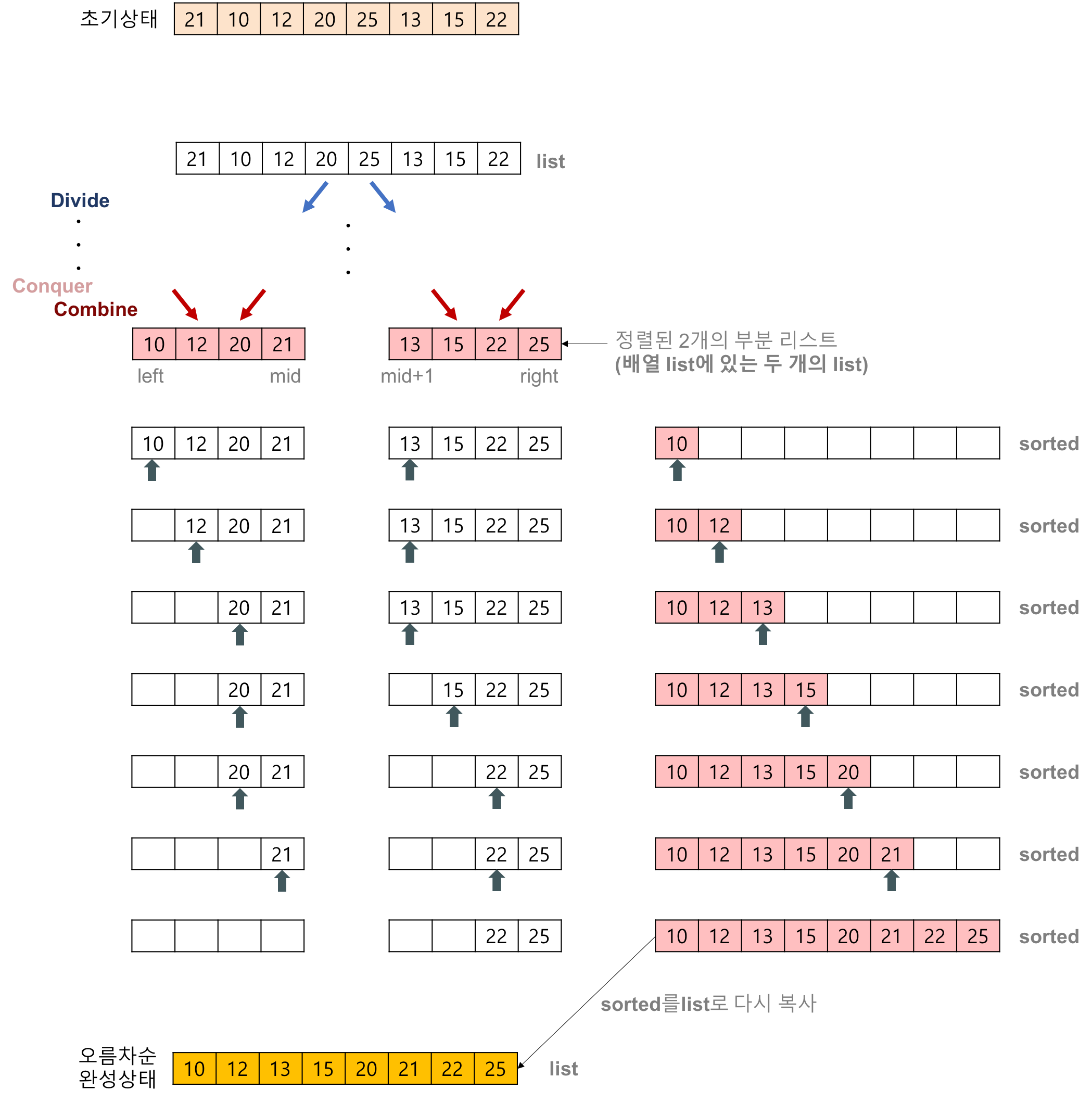
합병 및 정렬 수행 예시: https://gmlwjd9405.github.io/ 에서 발췌

최종 코드

# 병합 정렬
## 분할
merge_sort <- function(x) {
  n <- length(x)
  if (n > 1) {
    mid <- ceiling(n/2)
    left <- merge_sort(x[1:mid])
    right <- merge_sort(x[(mid + 1):n])
    smerge(left, right)
  } else {
    x
  }
}

## 병합 및 정렬
smerge <- function(left, right) {
  n1 <- length(left)
  n2 <- length(right)
  temp <- numeric(n1 + n2)
  lstart <- rstart <- 1
  for (i in 1:length(temp)) {
    if ((left[lstart] <= right[rstart] & 
        lstart <= length(left)) || 
        rstart > length(right)) {
      temp[i] <- left[lstart]
      lstart <- lstart + 1
    } else {
      temp[i] <- right[rstart]
      rstart <- rstart + 1
    }
  }
  temp
}

set.seed(12345)
x <- sample(1:100, 20)
x_sort <- merge_sort(x)

시간 복잡도

재귀함수의 깊이(\(n = 2^k\)로 가정):

단계 1: \(n/2\)

단계 2: \(n/2^2\)

\(\ldots\)

단계 k: \(n/2^k \rightarrow k\) 번까지 반복

\(\rightarrow\) 최악의 경우 \(n/2^k = 1\) 이므로 양변에 로그를 취하면 \(\log_2n\) 임. 각 합병 단계에서

\(n = 8\)인 경우 크기가 1인 부분 벡터 2개를 병합 시 최대 2 번의 연산이 필요하고, 부분 배열의 쌍이 4개이기 때문에 최대 \(2\times 4= 8\) 번의 비교 연산이 필요

다음 단계에서 병합 시 길이가 2인 부분 벡터 2 개 병합 시 4 번의 비교 연산이 필요하고 부분 벡터의 쌍이 2이기 때문에 최대 \(4\times 2= 8\) 번의 비교 연산 필요

마지막 단계에서 길이가 4인 부분 벡터 2개 병합 시 8 번의 비교 연산이 필요하고, 부분 벡터의 쌍이 1이기 때문에 최대 \(8\times 1= 8\) 번의 연산 필요

\(\rightarrow\) 최대 \(n\) 번

\(\therefore\) \(n\times \log_2n = n\log_2n\)

이동횟수

재귀함수의 깊이: \(\log_2 n\)

임시 벡터에 복사 후 다시 가져와야 하기 때문에 총 부분 배열에 들어 있는 원소의 개수가 \(n\)인 경우 원소의 이동이 총 \(2n\) 번 발생

\(\therefore\) \(2n\log_2 n\)

따라서 총 시간 복잡도는

\(n\log_2n + 2n\log_2n = 3n\log_2n \rightarrow \mathcal{O}(n\log_2n)\)

6.4.4 퀵 정렬(Quick Sort)

주어진 벡터(배열)을 단순히 균등하게 분할하는 대신 병합 과정 없이 한쪽 벡터에 포함된 원소가 다른 쪽 벡터에 포함된 원소보다 항상 작게 배열을 분할하는 방식으로 정렬을 수행함. 벡터에서 임의의 원소를 기준(pivot)으로 정한 후 기준보다 작거나 같은 원소는 왼쪽, 큰 원소는 오른쪽으로 보내는 과정을 수행

불안정 정렬
분할 정복 알고리즘 중 하나로 매우 좋은 효율을 보임
다른 원소와 비교를 재귀적으로 수행 \(\rightarrow\) 비교 정렬
병합 정렬과 달리 주어진 벡터(배열)을 비균등하게 분할

Quick 정렬 애니메이션: 위키피디아 발췌

퀵 정렬 과정

벡터 내 한 원소를 임의로 선택 \(\rightarrow\) 피벗(pivot)
피벗을 기준으로 피벗보다 작은 원소는 모두 피벗의 왼쪽으로 옮기고, 피벗보다 끈 원소들은 모두 오른쪽으로 옮김 \(\rightarrow\) 분할
피벗을 제외한 왼쪽과 오른쪽 부분 벡터를 정렬 \(\rightarrow\) 정복
- 분할된 부분 벡터에 대해 재귀호출을 통해 정렬 반복
- 부분 벡터에 대해서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 벡터로 나누는 과정 반복
부분 벡터들이 더 이상 분할할 수 없을 때 까지 반복
- 벡터의 크기가 1이 될 때 까지 반복
정렬한 부분 벡터를 하나의 벡터로 병합 \(\rightarrow\) 결합

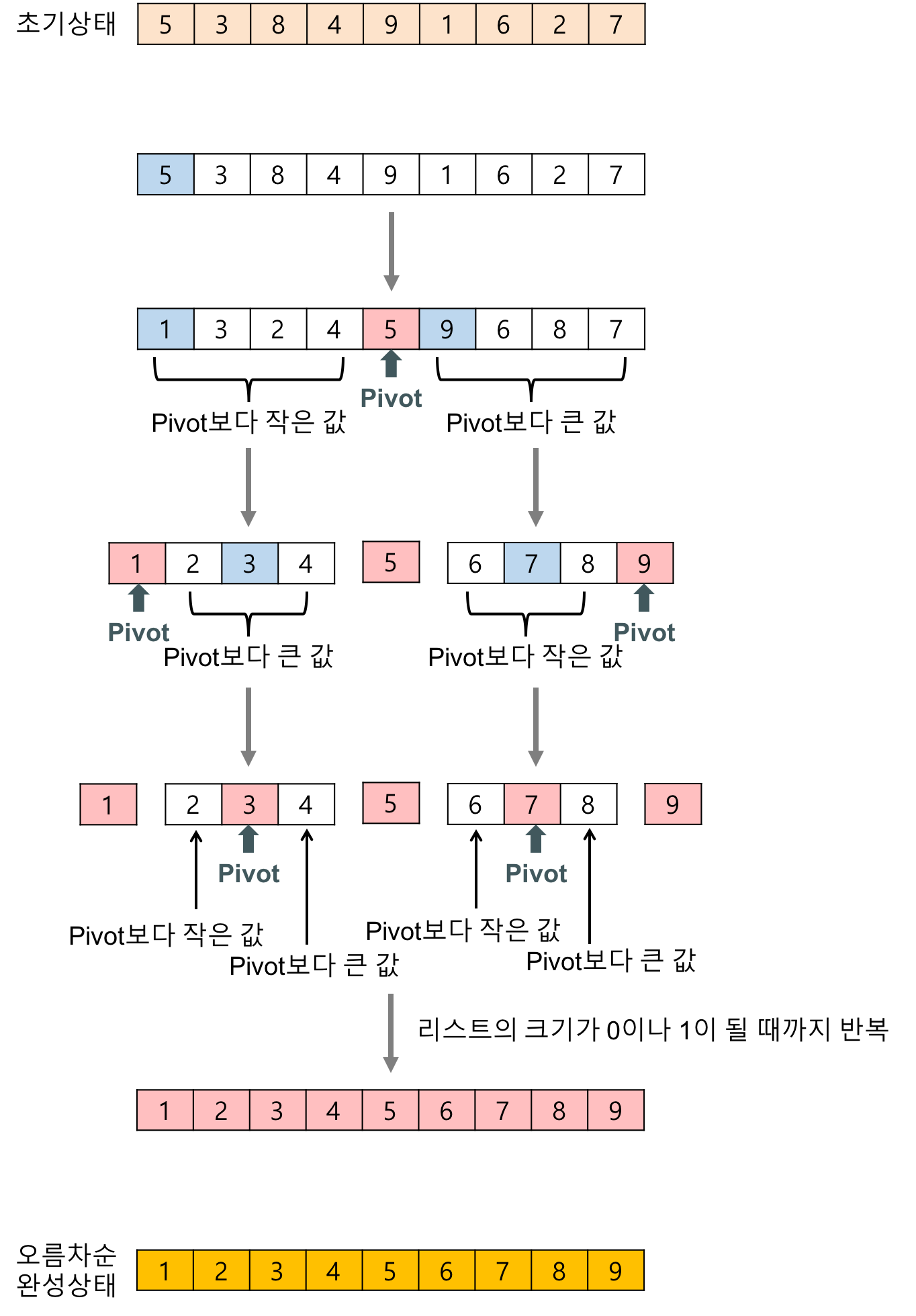
Quick 정렬 알고리즘 과정: https://gmlwjd9405.github.io/ 에서 발췌

특징

장점

속도가 빠름
추가 메모리 공간을 필요로 하지 않음
\(\mathcal{O}(\log_2 n)\) 만큼의 메모리 필요

단점

정렬된 벡터(배열)에 대해서는 불균형 분할로 인해 수행시간이 더 오래 걸림

구현

재귀함수를 이용한 퀵 정렬 알고리즘 구현

Pseudocode

quicksort(x)

pivot 선택

left = x[x <= pivot]; right = x[x > pivot]

if (l < 1) then quicksort(left)

if (r < 1) then quicksort(right)

merge (left, pivot, right)

# Quick 정렬
quick_sort <- function(x) {
  n <- length(x)
  randi <- sample(1:n, 1)
  pivot <- x[randi]
  x <- x[-randi]
  
  # 피벗을 기준으로 작은 값들은 left, 
  # 큰 값은 right 로 분할
  left <- x[which(x <= pivot)]
  right <- x[which(x > pivot)]
  
  # left에 대해 재귀적으로 분할 
  if (length(left) > 1) left <- quick_sort(left)
  if (length(right) > 1) right <- quick_sort(right)
  out <- c(left, pivot, right)
  out
}

x <- sample(1:100, 20)
quick_sort(x)

 [1]  1  3  9 12 13 14 16 20 25 30 32 36 60 62 64 72 75 76 80 84

시간 복잡도

최선의 경우
- pivot 좌우로 분할된 벡터의 크기가 각 재귀 단계마다 동등한 경우, 재귀 단계에 대한 깊이는 병합 정렬과 동일하게 \(\log_2 n\) 임.
- 각 재귀 단계에서 비교 연산은 전체 \(n\) 번의 비교가 필요
- \(\therefore\) \(\mathcal{O}(n\log_2 n)\)
최악의 경우
- 정렬된 벡터에서 계속해서 불균형하게 분할이 이루어지는 경우, 재귀 단계의 깊이는 최대 \(n\) 임
- 각 재귀 단계에서 비교는 전체 \(n - 1\) 만큼 이루어짐
- \(\therefore\) \(\mathcal{O}(n^2)\)

Big-O 표기법에 따르면 퀵 정렬의 시간 복잡도는 \(\mathcal{O}(n^2)\) 인데, 왜 빠르다고 할까??